目次
はじめに
こんにちは。AIシステム技術部のK山です。
前回はAIと統計学の関係について調べ、AIを開発するにはまず統計学が必要だということが分かりました。
今回は統計学の第2回目ということで、

今回から、手法について書いていってね。

分かりました。
それでは、手法について調べていきます。
調べたところ、よく使われるのは以下の手法のようです。
分散分析
t検定
多重比較法
点推定
主成分分析
重回帰分析

どうしてこんなに多いのでしょうか…
知りたい結果によって手法を使い分けるということでしょうか。

1つずつ特徴を調べていこうと思います。
まず「点推定」について調べたところ、以下のような解説文を見つけました。
母平均は「標本平均」で推定する。
これは、母平均を1点でズバリと推定しています。このような推定方法を「点推定」といいます。引用元:大上丈彦(2012年)
『マンガでわかる統計学【素朴な疑問からゆる~く解説】』
SBクリエイティブ出版(P174)
上記の引用文だけではイメージしにくいですが、併せて載っていた図を見たらわかりやすかったです。
それをもとにして図を作ってみました。
以下の図は、ある大量のデータから平均を求めたいときのケースになります。
もし、データをとる対象が何千もある場合、1つ1つのデータを収集するのが大変ですし、収集中にデータが変わってしまうこともあります。
例えば、日本人男性の平均身長を割り出したいとき、国民全員の身長を調べよう、なんて現実的ではないです。それに、身長は伸びるのでデータに変動が起こってしまいます。
なので、「とれる分のデータで、平均身長を予想するしかないよ」となるわけです。
つまり点推定とは、一部のデータをもとにして、全体を推定する手法なのです。

テストの点数結果を例として挙げると以下のようなイメージです。
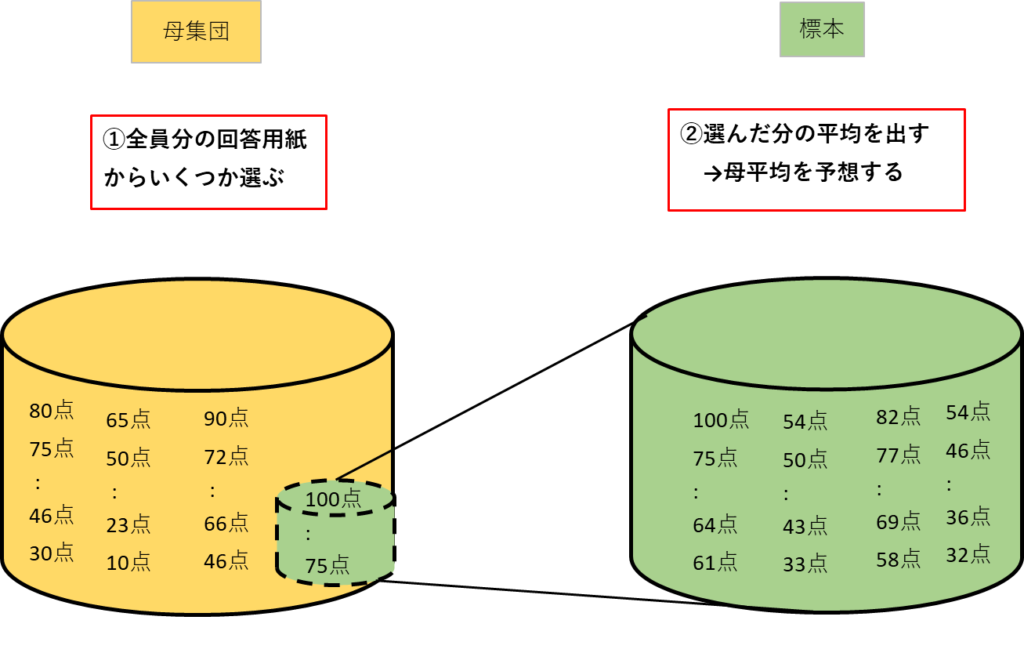
ちなみに、平均値の他に中央値・最頻値を求める際も点推定が使われるそうです。
中央値は、大きさ順に並べたときに真ん中に位置する値のことで、
最頻値は、母集団の中で一番多く存在する値のことです。
平均値は身近で、一番わかりやすいかと思ったので、例にあげました。

身近な例で考えてみたら、なんとなく理解できました。
このように目的が分かれば、手法をイメージしやすいと思います。

まずは、それぞれの目的から探ってみましょう。
統計学の目的とは
そもそも、統計学の目的とはなんでしょうか?
調べたところ、下記の記述を見つけました。
統計学とは、ある1つの群のデータに対してその性質を調べたり、あるいは手持ちのデータからもっと大きな未知のデータや未来のデータを推測するための学問です。
上記の記述から、2つの目的が考えられますね。
・調べる
・推測する
この2つの目的を、前回記述した5つの用途に照らし合わせてみました。
| 【調べる】 ・検定 →確率をもとに結論を導く方法 例)占い師が5回連続で占いを的中させたがそれで本物であるといえるのかを検証 ・要約 →データを1つの数値にまとめる方法 例)テストの平均点は何点か、一番高い点数は何点かなど |
| 【推測する】 ・推定 →一部の手持ちデータを分析し、まだ手にしていない全体のデータの特徴を推測する方法 例)ランダムで選んだ日本人男性100人の平均身長は165cmだったので、 日本人男性の平均身長は165cmだ ・予測 →手持ちのデータから未来を予測する方法 例)今から1時間ランニングをしたら、何キロやせるだろうか |
| ・確率 →物事の確率を求める方法 例)サイコロを振って1が出る確率 |
前回のブログでは、確率は統計学に使われているため用途の一つだと記載しました。
ですが目的に照らし合わせて考えてみると、用途の一つではなく用途に付属しているもの、のように思います。
※第1回目ブログの「統計学の用途」にて訂正しています。
下記の図のようなイメージです。
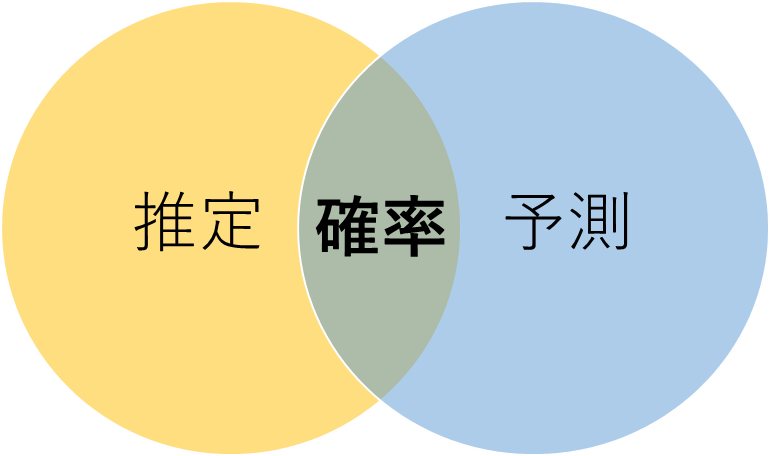
検定は確率をもとに結論を導く手法だと書きましたが、推定・予測に関しても、確率が必須になります。
確率とはあることが起きるであろう割合を数字で表したものになり、統計学は確率で表したものを使ってさらに分析するものです。
よって、確率は用途ではなく、分析する上で必要な道具の一つと言えるでしょう。
手法をグループ分けしてみた
6つの手法を、それぞれ目的ごとに分けてみました。
| 【調べる】 ・検定 →確率をもとに結論を導く方法 例)占い師が5回連続で占いを的中させたがそれで本物であるといえるのかを検証 手法:T検定,分散分析,多重比較法 ・要約 →データを1つの数値にまとめる方法 例)テストの平均点は何点か、一番高い点数は何点かなど 手法:主成分分析 |
| 【推測する】 ・推定 →一部の手持ちデータを分析し、まだ手にしていない全体のデータの特徴を推測する方法 例)ランダムで選んだ日本人男性100人の平均身長は165cmだったので、 日本人男性の平均身長は165cmだ 手法:点推定 ・予測 →手持ちのデータから未来を予測する方法 例)今から1時間ランニングをしたら、何キロやせるだろうか 手法:重回帰分析 |
さて、代表的な手法を用途ごとに分けてみましたが、検定の手法だけかなりかぶってしまいました…
手法の名前だけを見ると別物ではないかと思いますが、用途は同じですよね。
何か理由があって、手法を使い分けるのでしょうか?
分散分析、T検定、多重比較法の違いを軽く調べてみたところ、
以下のことが分かりました。
T検定→2つのデータの平均値を比較ときに使う
分散分析→3つ以上のデータの平均値を比較するときに使う
多重比較法→分散分析の結果よりさらに詳しいことが分かる
分散分析を行った後に使われることが多い
なるほど…同じ用途であっても、条件によっては使えなかったり、手法によって得られる結果の量も違うみたいですね!
他の用途にも、対応する手法が複数あるかもしれませんね。
本ブログでは、代表的な手法を紹介するので、提示した6つの手法以外については書きませんが、他の手法を調べてみるのも面白そうです。
今回、手法の概要をざっくり理解してから、手順を調べてみるという目的で、統計学の目的から段階的に書いていきました。
仲間分けをしたことで、似ている手法があること、それらの使い分けもわかったので、次回からはスムーズに説明ができそうです。
総論
今回のブログでは、手法について調べ、実際の手順までを書いていこうと思っていました。
ですが、用語の意味が分からない状態で手順を調べたため、なんとなくでしかイメージがつかめなかったのと、そもそも何のために手法を使うのか理解する必要があると思い、途中からブログ内容を変更しました。
目的と手法を仲間分けしたことで、それぞれの手法で得られる結果や特徴のイメージを掴むことができました。
また、初めから疑問に思っていた「手法が多い理由」に関しても、以下の点で使い分けるためだということが分かりました。
・目的
・用途
・ほしい結果の粒度
次回からは、いよいよ各手法について書いていきます。
せっかく仲間分けしたので、同じ用途で使われる手法を一緒に紹介したいと思います。
次回は下記の手法について調べていきます。
【 検 定 】
・分散分析
・T検定
・多重比較法

